2장-(3)랭크

차원정리

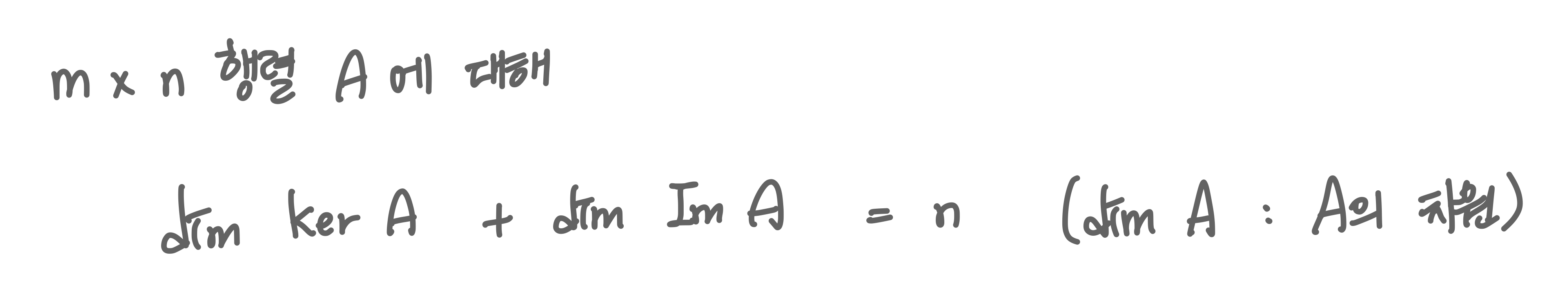
*Ker A의 차원이 k라고 했을 때, 이는 Ker A의 기저가 k개의 벡터로 이루어진다는 것을 의미하고 Im A의 차원도 마찬가지이다. 

 

 

선형독립, 선형종속

"납작하게 눌린다"는 것의 의미는 "서로 다른 x와 x'가 같은 y로 이동한다"는 것이다. 수식을 이용하여 표현해 보면 아래와 같다.

선형독립 / 선형종속

• A의 열벡터들이 선형종속 = 납작하게 눌린다
• A의 열벡터들이 선형독립 = 납작하게 눌리지 않는다

 

 

랭크

랭크는 단서의 실질적인 개수라고 생각하면 된다. 이것은 "상 Im A가 공간 전체를 커버하고 있는가"에 대해 조사해야하기 때문에 자연스럽게 그 차원인 dim Im A이며, rank A 라는 기호를 사용한다. 또한 앞서 설명한 차원정리를 통해 "납작하게 눌리는가"에 관한 정보인 Ker A의 차원 수도 알 수 있다. (*랭크를 계수라고 부르는 경우도 있음)

 

랭크의 기본성질

A가 m X n 행렬이라면,

 

*전치해도 랭크는 동일함

 

랭크 구하는 방법

A가 m X n 행렬일때 A로 이동하는 범위인 Im A는 "n차원 벡터 x를 여러모로 움직이는 경우 y = Ax의 움직일 수 있는 범위"이다. 이것을 span을 사용하여 표기하고 벡터가 만드는 선형 부분공간이라고 부른다. 

 

랭크의 기본 성질에 따라 정칙행렬을 곱해도 랭크는 변하지 않으므로, "정칙행렬을 계속 곱하여 행렬을 간단하게 한 뒤 한눈에 랭크를 알 수 있는 모양으로 바꾸자"는 흐름으로 진행된다. 완성된 행렬의 1의 개수가 랭크이다.