Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- 정칙행렬
- 연립일차방정식
- 딥러닝
- word embedding
- ReLU
- Linear Algebra
- Python
- one-hot vector
- 벡터간 유사도
- word2vec
- pandas
- sigmoid
- SVD
- 밑바닥부터 시작하는 딥러닝
- PPMI
- 역행렬
- machine translation
- RNN
- 프로그래머를 위한 선형대수
- Transformer
- 자연어처리
- NMT
- DataFrame
- 동시발생 행렬
- 밑바닥부터 시작하는 딥러닝2 2장
- 선형대수학
- 판다스
- 신경망 학습
- 데이터프레임
- NLP
Archives
- Today
- Total
생각하는감자
4장-(2) 요르단 표준형 본문
요르단 표준형
대각화가 불가능한 정방행렬 A라도 대각에 가까운 요르단 표준형이라면 변환할 수 있다. A를 요르단표준형으로 변환한다는 것인데, 요르단 표준형은 아래와 같은 모양이다.
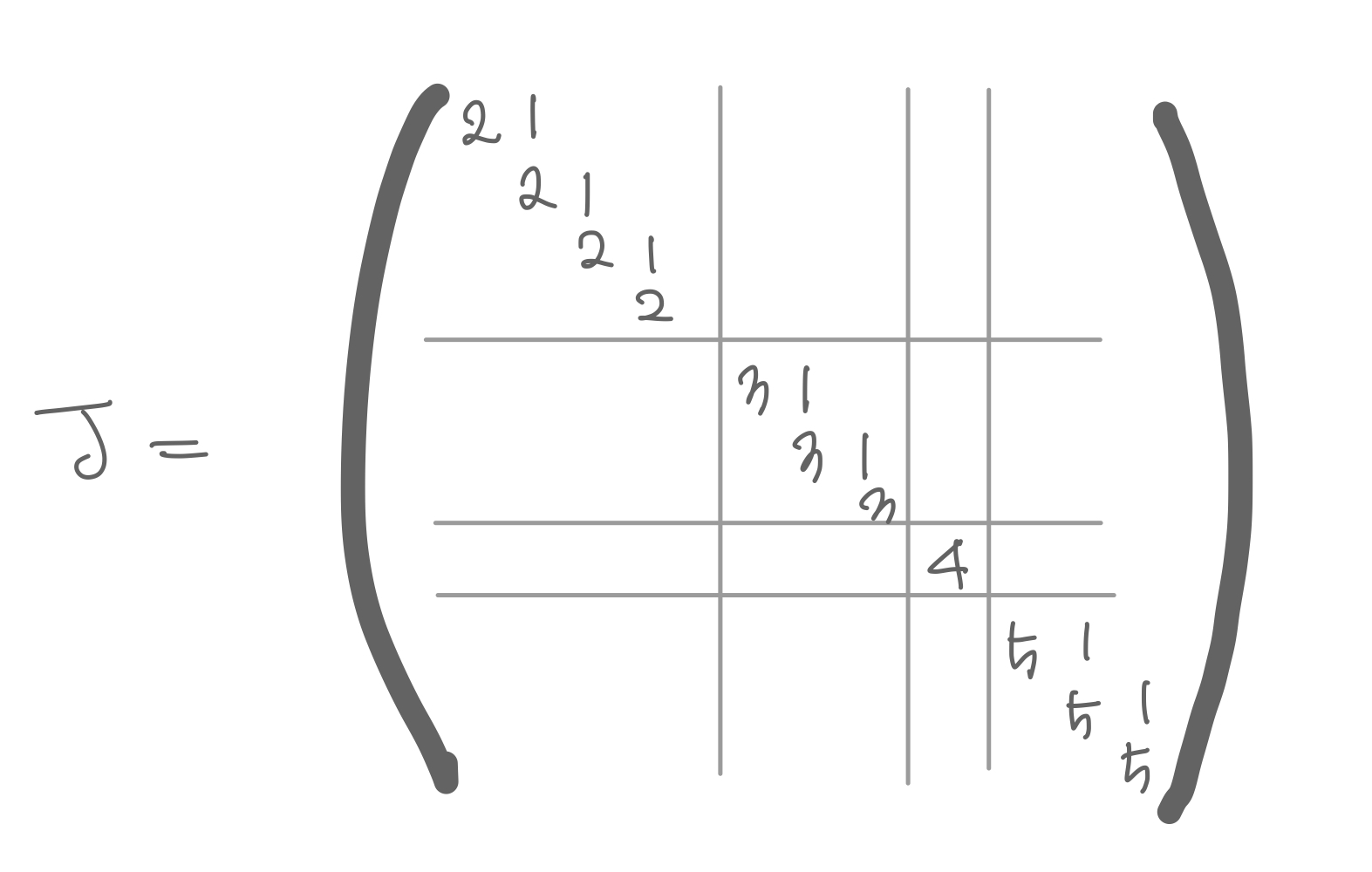
- 블록정방행렬이고, 대각블록 이외에는 모두 0이다.
- 대각블록은
- 대각 성분에 같은 수가 나열되어 있으며,
- 하나 오른쪽 위에는 1이 비스듬히 늘어서있는 특징을 가지고 있다.
요르단 표준형의 성질
요르단 표준형의 주요 장점은
- 고윳값과 고유벡터의 모양이 보인다는 것과
- 거듭제곱을 구체적으로 계산할 수 있다는 것이다.
요르단 표준형에서
- 대각성분 = 고윳값
- 대각성분의 개수 = 대수적 중복도(고윳값이 몇 중해인지)
- 요르단 셀의 개수가 고윳값에 선형독립인 고유벡터 개수에 대응(기하적 중복도)
*고윳값에 중해가 없을 경우에는 대각화가 가능하다. 대각행렬이 될 수밖에 없다.*
요르단 표준형 구하는 법

'선형대수학' 카테고리의 다른 글
| SVD(1) (0) | 2023.03.27 |
|---|---|
| 4장-(1)대각화, 고윳값, 고유벡터 (0) | 2023.03.24 |
| 3장-LU분해 (0) | 2023.03.23 |
| 2장-(4)성질의 좋고 나쁨의 판정 (0) | 2023.03.23 |
| 2장-(3)랭크 (0) | 2023.03.23 |




